Equilibria and their stable/unstable manifolds teach us a lot about the geometry of the state space, but as they are stationary, no turbulence takes place there. As the following dual-view movies show, the time dependence of typical unstable structures seen in turbulence is better captured by unstable periodic orbits embedded in the turbulent regions of the state space.
(if flash does not play: mp4 format, 1.3 MB)
P35 (black line in the above, purple dots line in the figure below) is a relative periodic orbit: the field returns to a streamwise half-cell translation in x of its original state after one period (T=35.86), and then to its original state after two periods (T=71.72).
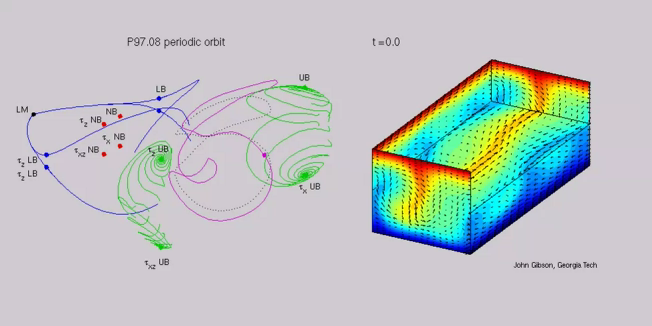
The P97 orbit (purple line) is a periodic orbit close to a two-period repeat of the P35 orbit, with an extra wiggle; it is the beginning of the infinite hierarcy of unstble periodic orbits embedded in the turbulent flow. From the 3D video it would be hard to tell that this is not a segment of a typical turbulent orbit - it captures well the typical coherent structures observed in earlier videos. (I have not reached conclusive convergence on this orbit; it still might be just a close recurrence).