
 |
 |
 |
 |
Accurate description of the dynamics is crucial for a number of fundamental and applied problems involving nonequilibrium systems, such as calculation of transport properties or control of unstable patterns. Due to the intrinsic nonlinearities and high dimensionality, analytic description of spatiotemporally chaotic (STC) dynamics is in general impossible. The tools of statistical mechanics and low-dimensional dynamical systems theory are not directly applicable either; a whole new approach to characterization of STC needs to be developed. The main idea of such an approach is based on the fact that, due to natural dissipation, only a relatively small number of degrees of freedom are active, such that asymptotically the dynamics is confined to a finite-dimensional invariant manifold. The two main goals of our research in STC are to identify the relevant degrees of freedom and to construct a dynamically and statistically accurate description. For instance, symmetry analysis could be used to reduce the problem dimensionality by factoring out the degeneracies associated with spatial invariance.
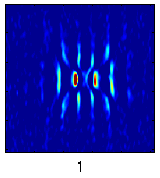
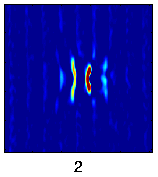
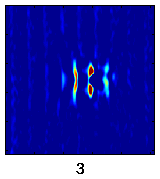
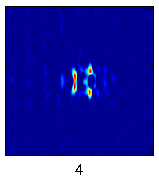
A related study focuses on generic localized spatiotemporal instabilities to develop novel ways to extract relevant information from experimental data. For instance, experimental data (shadowgraphic images of the depth-averaged temperature field) for spiral defect chaos in Rayleigh-Benard convection (left figure below) can be used to extract the information about the effective degrees of freedom describing certain characteristic types of spatiotemporal instabilities. The figures (below right) show the spatial structure of the four dominant modes excited in the process of pinching of one of the convection rolls, leading to the formation of two dislocation defects (yellow arrows in the left figure).
 |
|
Take a look at M. Schatz's
Spiral Defect Chaos webpage for more pictures.
Go back to Home Page