A class to calculate the periodic eigendecomposition of the product of a sequence of matrices. More...

#include <ped.hpp>

Public Member Functions
MatrixXd	EigVals (MatrixXd &J, const int MaxN=100, const double tol=1e-16, bool Print=true)
	Eigvals() calculate the eigenvalues of the product of a sequence of matrices in the form of 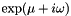$\exp(\mu+i\omega)$ .
pair< MatrixXd, MatrixXd >	EigVecs (MatrixXd &J, const int MaxN=100, const double tol=1e-16, bool Print=true)
	calculate the eigenvectors of the product of a sequence of matrices
std::tuple< MatrixXd, vector < int >, MatrixXd >	eigenvalues (MatrixXd &J, const int MaxN=100, const double tol=1e-16, bool Print=true)
	calculate the periodic Schur decomposition and the eigenvalues of the product of a sequence of matrices.
pair< MatrixXd, vector< int > >	PerSchur (MatrixXd &J, const int MaxN=100, const double tol=1e-16, bool Print=true)
	Periodic Schur decomposition of a sequence of matrix stored in J.
MatrixXd	HessTrian (MatrixXd &G)
vector< int >	PeriodicQR (MatrixXd &J, MatrixXd &Q, const int L, const int U, const int MaxN, const double tol, bool Print)
void	Givens (Ref< MatrixXd > A, Ref< MatrixXd > B, Ref< MatrixXd > C, const int k)
void	Givens (Ref< MatrixXd > A, Ref< MatrixXd > B, Ref< MatrixXd > C, const Vector2d &v, const int k)
	Givens rotation with provided 2x1 vector as parameter.
void	HouseHolder (Ref< MatrixXd > A, Ref< MatrixXd > B, Ref< MatrixXd > C, const int k, bool subDiag=false)
void	GivensOneIter (MatrixXd &J, MatrixXd &Q, const Vector2d &v, const int L, const int U)
void	GivensOneRound (MatrixXd &J, MatrixXd &Q, const Vector2d &v, const int k)
vector< int >	checkSubdiagZero (const Ref< const MatrixXd > &J0, const int L, const int U, const double tol)
vector< int >	padEnds (const vector< int > &v, const int &left, const int &right)
	pad two elements at the begining and end of a vector.
double	deltaMat2 (const Matrix2d &A)
	return the delta of a 2x2 matrix : for [a, b c, d] Delta = (a-d)^2 + 4bc
Vector2d	vecMat2 (const Matrix2d &A)
	calculate the eigenvector of a 2x2 matrix which corresponds to the larger eigenvalue. Note: MAKE SURE THAT THE INPUT MATRIX HAS REAL EIGENVALUES.
pair< Vector2d, Matrix2d >	complexEigsMat2 (const Matrix2d &A)
	get the eigenvalues and eigenvectors of 2x2 matrix
int	sgn (const double &num)
	return the sign of double precision number.
pair< double, int >	product1dDiag (const MatrixXd &J, const int k)
pair< Matrix2d, double >	product2dDiag (const MatrixXd &J, const int k)
vector< int >	realIndex (const vector< int > &complexIndex, const int N)
	realIndex() gets the positions of the real eigenvelues from the positions of complex eigenvalues.
vector< Triplet< double > >	triDenseMat (const Ref< const MatrixXd > &A, const size_t M=0, const size_t N=0)
	triDenseMat() creates the triplets of a dense matrix
vector< Triplet< double > >	triDenseMatKron (const size_t I, const Ref< const MatrixXd > &A, const size_t M=0, const size_t N=0)
	triDenseMat() creates the triplets of the Kroneck product of an IxI identity matrix and a dense matrix: Identity x R
vector< Triplet< double > >	triDiagMat (const size_t n, const double x, const size_t M=0, const size_t N=0)
	triDiagMat() creates the triplets of a diagonal matrix.
vector< Triplet< double > >	triDiagMatKron (const size_t I, const Ref< const MatrixXd > &A, const size_t M=0, const size_t N=0)
	triDiagMat() creates the triplets of the product of a matrix and an IxI indentity matrix.
pair< SparseMatrix< double > , VectorXd >	PerSylvester (const MatrixXd &J, const int &P, const bool &isReal, const bool &Print)
	perSylvester() create the periodic Sylvester sparse matrix and the dense vector for the reordering algorithm.
MatrixXd	oneEigVec (const MatrixXd &J, const int &P, const bool &isReal, const bool &Print)
	calculate eigenvector corresponding to the eigenvalue at postion P given the Periodic Real Schur Form.
void	fixPhase (MatrixXd &EigVecs, const VectorXd &realComplexIndex)
	fix the phase the complex eigenvectors
void	reverseOrder (MatrixXd &J)
	Reverse the order of columns of a matrix.
void	reverseOrderSize (MatrixXd &J)
	Reverse the order of a matrix and also resize it.

Detailed Description

A class to calculate the periodic eigendecomposition of the product of a sequence of matrices.

Note:: This class require c++0x or c++11 support.

Member Function Documentation

pair< Vector2d, Matrix2d > PED::complexEigsMat2 ( const Matrix2d & A )

get the eigenvalues and eigenvectors of 2x2 matrix

Eigenvalue is stored in exponential way : e^{mu + i*omega}. Here, omega is guarantted to be positive in [0, PI]. The real and imaginary parts are splitted for eigenvector: [real(v), imag(v)] Only one eigenvalue and corresponding eigenvector are return. The other one is the conjugate.

Example: for matrix [1, -1 1, 1], it returns [ 0.346, 0.785] and [-0.707, 0 0 0.707 ] Note : make sure that the input matrix has COMPLEX eigenvalues.

std::tuple< MatrixXd, vector< int >, MatrixXd > PED::eigenvalues	(	MatrixXd &	J,
		const int	MaxN = `100`,
		const double	tol = `1e-16`,
		bool	Print = `true`
	)

calculate the periodic Schur decomposition and the eigenvalues of the product of a sequence of matrices.

Returns:: A tuple consists of eigenvalues, position of complex eigenvalues and transform matrices.

MatrixXd PED::EigVals	(	MatrixXd &	J,
		const int	MaxN = `100`,
		const double	tol = `1e-16`,
		bool	Print = `true`
	)

Eigvals() calculate the eigenvalues of the product of a sequence of matrices in the form of 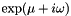$\exp(\mu+i\omega)$ .

It returns a [N,3] matrix, with the first column stores 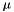$\mu$ , the second column stores 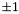$\pm 1$ for real eigenvalues or 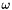$\omega$ for complex eigenvalues, and the third column states whether the eigenvalue is real (0) or complex (1).

Example usage:

 MatrixXd J3 = MatrixXd::Random(5,5);
 MatrixXd J2 = MatrixXd::Random(5,5); 
 MatrixXd J1 = MatrixXd::Random(5,5);
 MatrixXd J(5,15);
 J << J3, J2, J1;
 PED ped;
 MatrixXd eigvals = ped.Eigvals(J, 1000, 1e-16, false);
 cout << eigvals << endl << endl;

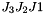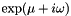The above code return the eigenvalues of $ J_3J_2J1$ in the format of $\exp(\mu+i\omega)$ .

Parameters:

[in]	MaxN	Maximal number of periodic QR iteration.
[in]	J	a sequence of matrices. Dimension [N, N*M].
[in]	tol	Tolerance used to check the convergence of the iteration process.
[in]	Print	Indicate whether to print the intermediate information.

Returns:: Matrix of size [N,3].

pair< MatrixXd, MatrixXd > PED::EigVecs	(	MatrixXd &	J,
		const int	MaxN = `100`,
		const double	tol = `1e-16`,
		bool	Print = `true`
	)

calculate the eigenvectors of the product of a sequence of matrices

Suppose Input matrix 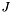$J$ is a sequence of matrices with the same dimension [N,N]: $[J_M, J_{M-1}, \cdots, J_1]$ . Function PED::EigVecs() will return you two matrices.

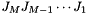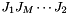The first one is the eigen-matrix, for the specific format, see PED::EigVals(). The second matrix has dimension [N*N, M]. The first column stores the eigenvectors of product $J_M J_{M-1}\cdots J_1$ stacked up-down $[v_1, v_2,\cdots,v_M]^{\top}$ . The second column stores the eigenvectors of product $J_1 J_{M}\cdots J_2$ , and similarly, for the remaining columns.

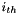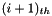Note:: For complex eigenvectors, they always appear in complex conjugate pairs. So, the real and imaginary parts are stored separately. For example, if the $i_{th}$ and $(i+1)_{th}$ vectors are complex pair, then elements from 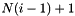to 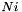is the real part, and elements from 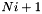to 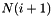is the imaginary part. They are stored in this way for better usage of memory.

Example usage:

 MatrixXd J3 = MatrixXd::Random(5,5);
 MatrixXd J2 = MatrixXd::Random(5,5); 
 MatrixXd J1 = MatrixXd::Random(5,5);
 MatrixXd J(5,15);
 J << J3, J2, J1;
 PED ped;
 std::pair<MatrixXd, MatrixXd> eigs = ped.Eigvals(J, 1000, 1e-16, false);
 cout << eigs.first << endl << endl; // print eigenvalues
 cout << eigs.second << endl << endl; // print eigenvectors.

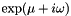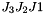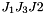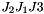The above code return the eigenvalues (in the format of $\exp(\mu+i\omega)$ ) and eigenvectors of $ J_3J_2J1$ , $ J_1J_3J2$ , $ J_2J_1J3$ .

Parameters:

[in]	MaxN	Maximal number of periodic QR iteration.
[in]	J	a sequence of matrices. Dimension [N, N*M].
[in]	tol	Tolerance used to check the convergence of the iteration process.
[in]	Print	Indicate whether to print the intermediate information.

Returns:: a pair of matrices storing eigenvalues and eigenvectors.

void PED::fixPhase	(	MatrixXd &	EigVecs,
		const VectorXd &	realComplexIndex
	)

fix the phase the complex eigenvectors

The complex eigenvectors got from periodic eigendecompostion are not fixed becuase of the phase invariance. This method will make the first element of each complex eigenvector be real.

Parameters:

[in,out]	EigVecs	Sequence of eigenvectors got from periodic eigendecomposition
[in]	realCompelxIndex	A vector indicating whether a vector is real or complex (third column of eigenvalues got fromx periodic eigendecomposition).

void PED::Givens	(	Ref< MatrixXd >	A,
		Ref< MatrixXd >	B,
		Ref< MatrixXd >	C,
		const Vector2d &	v,
		const int	k
	)

Givens rotation with provided 2x1 vector as parameter.

MatrixXd PED::oneEigVec	(	const MatrixXd &	J,
		const int &	P,
		const bool &	isReal,
		const bool &	Print
	)

calculate eigenvector corresponding to the eigenvalue at postion P given the Periodic Real Schur Form.

The eigenvectors are not normalized, and they correspond to matrix products: JmJm-1..J1, J1JmJm-1..J2, J2J1Jm...J3, ...

vector< int > PED::padEnds	(	const vector< int > &	v,
		const int &	left,
		const int &	right
	)

pad two elements at the begining and end of a vector.

vector< int > PED::PeriodicQR	(	MatrixXd &	J,
		MatrixXd &	Q,
		const int	L,
		const int	U,
		const int	MaxN,
		const double	tol,
		bool	Print
	)

PeriodicQR transforms an unreduced hessenberg-triangular sequence of matrices into periodic Schur form. This iteration method is based on the Implicit-Q theorem.

pair< MatrixXd, vector< int > > PED::PerSchur	(	MatrixXd &	J,
		const int	MaxN = `100`,
		const double	tol = `1e-16`,
		bool	Print = `true`
	)

Periodic Schur decomposition of a sequence of matrix stored in J.

Returns:: pair value. First is the orthogonal transform matrix sequence Qm, Qm-1,..., Q1 Second is the vector storing the positions of complex eigenvalues.

pair< SpMat, VectorXd > PED::PerSylvester	(	const MatrixXd &	J,
		const int &	P,
		const bool &	isReal,
		const bool &	Print
	)

perSylvester() create the periodic Sylvester sparse matrix and the dense vector for the reordering algorithm.

Parameters:

J	the sequence of matrix in order: Jm, Jm-1,... J1
P	the position of the eigenvalue
isReal	for real eigenvector; otherwise, complex eigenvector

vector< int > PED::realIndex	(	const vector< int > &	complexIndex,
		const int	N
	)

realIndex() gets the positions of the real eigenvelues from the positions of complex eigenvalues.

Denote the sequence of complex positions: [a_0, a_1,...a_s], then the real positions between [a_i, a_{i+1}] is from a_i + 2 to a_{i+1} - 1. Example: Complex positions : 3, 7, 9 Dimension : N = 12 ==> Real positions : 0, 1, 2, 5, 6, 11

void PED::reverseOrder ( MatrixXd & J )

Reverse the order of columns of a matrix.

J = [j1,j2,...jm] => [Jm, jm-1, ..., j1]

Parameters:

[in,out] the matrix that need to be reversed in place.

See also:: reverseOrderSize()

void PED::reverseOrderSize ( MatrixXd & J )

Reverse the order of a matrix and also resize it.

We usually squeeze the input such that each column represents one of the members of a sequence of matrices. reverseOrderSize() will first reverse the order and then resize it to the right format. Eg: [j1,j2,...jm] => [jm jm-1,...j1] with dimension [N^2, M] => dimension[N,N*M]

Parameters:

[in,out] J The matrix that need to be reversed and re-sized in place.

See also:: reverseOrder()

vector< Tri > PED::triDenseMat	(	const Ref< const MatrixXd > &	A,
		const size_t	M = `0`,
		const size_t	N = `0`
	)

triDenseMat() creates the triplets of a dense matrix

vector< Tri > PED::triDenseMatKron	(	const size_t	I,
		const Ref< const MatrixXd > &	A,
		const size_t	M = `0`,
		const size_t	N = `0`
	)

triDenseMat() creates the triplets of the Kroneck product of an IxI identity matrix and a dense matrix: Identity x R

vector< Tri > PED::triDiagMat	(	const size_t	n,
		const double	x,
		const size_t	M = `0`,
		const size_t	N = `0`
	)

triDiagMat() creates the triplets of a diagonal matrix.

vector< Tri > PED::triDiagMatKron	(	const size_t	I,
		const Ref< const MatrixXd > &	A,
		const size_t	M = `0`,
		const size_t	N = `0`
	)

triDiagMat() creates the triplets of the product of a matrix and an IxI indentity matrix.

The documentation for this class was generated from the following files:

Public Member Functions

Detailed Description

Member Function Documentation